Установи соответствие между графиком и формулой линейной функции

Учим свойства логарифмов

    Чтобы хорошо запомнить свойства логарифмов, предлагаю провести лягушку на лист кувшинки.

     Для начала игры, нажмите на лягушку. С помощью клавиш управления курсором помогите лягушке выбрать то бревно, на котором записано выражение, соответствующее выражению на кувшинке. Постарайтесь не ошибаться, т.к. иначе лягушка или упадет в воду, или достанется на обед голодным змеям. В игре 20 уровней. Постарайтесь пройти все.

Проверяем как мы знаем свойства логарифмов

     Тренажер, позволяющий сначала запомнить, а потом проверить, насколько хорошо вы знаете свойства логарифмов. Подбирая подходящие пары карточек, постарайтесь открыть их все за минимальное время.

Тренажер устного счета от МетаШколы

Хороший тренажер, чтобы считать устно и без ошибок.

1. Выберите вид тренировки в выпадающем списке.
2. Нажмите кнопку "Начать тренировку".
3. На экране появится новый пример. Решите его и введите ответ в специальном поле.
4. Чтобы подтвердить ответ и перейти к следующему примеру, нажмите Enter (Ввод).
5. После правильного решения 10 примеров, Вы увидите диалоговое окно с результатами тренировки.

Логарифмы. Устный счет.

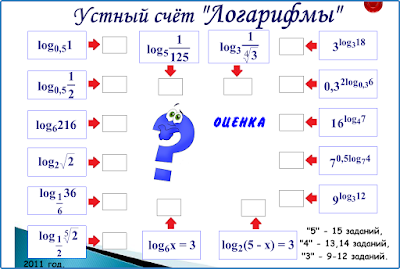     Проверить, как вы поняли и запомнили определение логарифма и основное логарифмическое  тождество, а самое главное, определить, как вы можете применять их на практике при вычислении логарифмов, поможет этот небольшой тренажер устного счета. Узнайте, можете ли вы двигаться дальше, или стоит вернуться к началу и повторить самое главное.

Счет на лету

     Отличная новость от сайта Учи.ру! на сайте появилась увлекательная обучающая игра по математике «Счёт на лету»! 

     Хотите считать быстро, хотите с пользой провести время за компьютером, стать чемпионом быстрого устного счета, тогда заходите почаще на эту страничку и с удовольствием тренируйтесь. Приглашаю  вас попробовать свои силы. Удачи!

Учимся вычислять логарифмы

     Продолжаем разбираться с логарифмами. Вам предлагается выполнить четыре задания, вычисляя логарифмы, пользуясь их определением и основным тригонометрическим тождеством. Задания лучше выполнять по-порядку, т.к. они идут по возрастанию сложности. В тренажере предусмотрена возможность делать заметки прямо в кадре. Успехов!

Вычисляем логарифмы

     После того, как мы разобрали определение логарифма, перейдем к их непосредственному вычислению. Все, что для этого нам нужно, это помнить, что как называется, знать таблицу умножения и уметь возводить число в степень.

    Допустим, нам надо вычислить log24 - вспоминаем, что логарифм это степень в которую нужно возвести основание логарифма, т.е. в нашем случае 2, чтобы получить число 4. Очевидно, что это 2. А раз 2² = 4, то и log24 = 2. Аналогично, log5125 = 3, т.к. 5³ = 125.
Потренируйтесь вычислять логарифмы с помощью тренажера.

 
Если у вас все получается, то попробуйте вычислить за одну минуту целых 40 логарифмов . Нажимайте на зеленую кнопку и вводите ответы в появившееся текстовое поле. Новый пример появляется только в случае вашего верного ответа.

Освоив принцип вычисления простых логарифмов можно переходить к более сложным примерам. Но перед этим, давайте вспомним, что операцию извлечения корня можно записать в виде степени с дробным показателем

. 

Воспользовавшись этим равенством, вычислим log93. 
Т.к. , то log93 = 1/2 = 0,5.
Иногда бывает сложно быстро подобрать ответ. В этом случае поступают следующим образом: Пусть нам необходимо вычислить log84. Обозначим log84 = х. По определению логарифма - . Т.к. 8 = 2³, а 4 = 2², то 23х = 2², откуда, решая показательное уравнение, будем иметь 3х = 2 и х = 2/3. Значит, log84 = 2/3.
Для решения еще одного типа логарифмов потребуется применить определение степени с отрицательным показателем:

.
Вычислим .
Заметим, что . Таким образом,

А теперь поработайте с тренажером khanacademy, и убедитесь, что вычислять логарифмы совсем не сложно.

     

      Чтобы окончательно убедиться, что тема освоена полностью, пройдите тест.

Что такое логарифм.

     Понятие логарифма многим кажется непонятным и сложным. На самом же деле все достаточно очевидно. Это просто другая, непривычная нам запись числа. Но, давайте разберемся по порядку.

     Предположим, что нам надо найти решение показательного уравнения 3x = 27. Для этого спросим себя: "В какую степень надо возвести 3, чтобы получить 27?" решаем методом подбора: три в первой - нет, три во второй - нет, три в третей - ДА!. Значит, тройку нужно возвести в третью степень, чтобы получить 27. Поэтому решением данного уравнения будет число три: x = 3.

А теперь попробуем решить другое уравнение 3x = 10. Здесь нам уже не удастся так просто подобрать красивое решение. Понятно, что x = 2, будет мало, а x = 3 будет много. Можно, конечно попробовать поискать приближенное решение. Но математики поступили по-другому. Они придумали особую запись числа для решения такого вида показательных уравнений и назвали их логарифмами. В нашем случае, решение уравнения 3x = 10 можно записать в виде log310 = x, то есть x - это число, в которое надо возвести 3, чтобы получить 10.

Теперь более общая запись: logab = c Читается так: «Логарифм по основанию a от b равен c», и означает: «Чтобы получить число b , нужно число a возвести в степень c»:

    

     

Итак: 

Логарифмом положительного числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число b

     Выражение 2³ = 8 
можно также записать в виде log28 = 3 . 
Читается это так: "Логарифм восьми по основанию два равен трем" или "Логарифм по основанию два от восьми равен трем".     
     Проанализируйте схему справа и постарайтесь разобраться с указанными стрелками переходами.

     Кстати, если вы внимательно посмотрите, то заметите, что и у степени числа и у логарифма основание всегда находится «ВНИЗУ». Легко запомнить правда? А вот «вверху», у степени находится ее показатель, а у логарифма – аргумент.

     Чтобы хорошо запомнить определение логарифма, предлагаю вам поработать с тренажером, расположенными ниже. Просто перетягивайте мышкой нужные цифры в подходящее поле. Полезно всякий раз проговаривать определение логарифма, это пригодится позднее при решении уравнений.

Logarithms

Применяем свойства подобных треугольников при решении задач

     Разобравшись с тем, какие треугольники называются подобными и повторив признаки подобия треугольников, можно приступать к решению задач. Два новых тренажера помогут вам выяснить, насколько хорошо усвоена данная тема.
     В первом предлагается восемь несложных примеров. Второй тренажер содержит более сложные задачи, но если вы сможете решить и их, значит проблем нет.  Можно смело сказать себе "Молодец!"
     Дерзайте!

 

Учим таблицу производных

     Чтобы хорошо запомнить таблицу производных, можно позаниматься с этим тренажером. Необходимо открыть все карточки, находя нужные пары, за минимальное время.

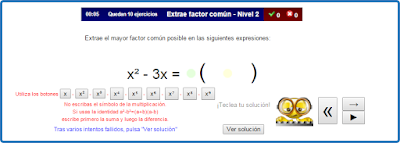
Вынесение одночлена за скобки

      Прежде чем сформулировать правило вынесения за скобки общего множителя, давайте вспомним, что многочлен - это алгебраическая сумма одночленов, а одночлен, в свою очередь, это произведение числа и степеней переменных. Вот среди этих чисел или степеней переменных и могут встретиться одинаковые общие множители, которые можно будет вынести за скобки. Так на рисунке мы видим три одночлена с общим множителем a·b. Если из этих одночленов составить многочлен 6a³b²c⁵ + 2a²bd - 3abc², то за скобки можно вынеси одночлен ab. При этом каждое слагаемое делится на выносимый множитель. 
Получим 6a³b²c⁵ + 2a²bd - 3abc² = ab(6a²bc⁵ + 2ad - 3c²).

С помощью смайликов составим схему, поясняющую процесс вынесения общего множителя за скобки:

Как видим, вынесение общего множителя за скобки осуществляется на основе распределительного закона умножения: ab + ac = a(b + c). 

 

Давайте рассмотрим, как проводить вынесение общего множителя за скобки, на конкретных примерах. Пример 1. 14a — 21b Начинаем с поиска общего множителя. Сначала ищем общий множитель среди чисел. Наибольшее число, на которое делится и 14, и 21 - это 7. Переменные a и b разные, общего множителя у них нет. Таким образом, общий множитель - 7. Вынести за скобки общий множитель - значит, поделить на этот множитель каждое слагаемое, стоящее в скобках. Делим на 7 сначала 14, затем 21.
Имеем: 14a - 21b = 7(2a - 3b).

Пример 2. 5у² + 10у И число 5, и число 10 делятся на 5, следовательно, общий множитель для чисел - пять. Из степеней у² и у выносим за скобки степень с меньшим показателем, то есть у (показатель 1 не пишем). Таким образом, в этом примере общий множитель равен 5у. Выносим его за скобки: при этом каждое слагаемое, стоящее в скобках, делим на этот множитель. Отдельно делим числа 5 и 10 на 5, отдельно — степени у² и у на у.
Получаем 5у² + 10у=5у(у + 2).

     Пример 3.      - 12a⁴b³c + 18a³b³c³ - 30a³b²c²

     Рассмотрим коэффициенты одночленов. Наибольшее число, на которое делятся числа 12, 18 и 30 - это 6. Поскольку первое слагаемое со знаком «-»,  выносим минус за скобки. При этом все знаки в скобках меняются на противоположные.

     Среди степеней a наименьшая a³.

     Среди степеней b - b².

     Среди степеней c - с в первой степени (пишем просто c).

     Таким образом, общий множитель  — это - 6a³b²c. Выносим его за скобки.

     Каждое слагаемое, стоящее в скобках, делим на этот множитель. При этом отдельно делим число на число, отдельно — степени с одинаковыми основаниями (показатели при этом вычитаются:

    12 : 6 = 2,  a⁴ : a³ = a,  b³ : b² = b,  c : c = 1,

    12a⁴b³c : 6a³b²c = 2ab;

    18 : 6 = 3,  a³ : a³ = 1,  b³ : b² = b,  c³ : c = c²,

    18a³b³c³ : 6a³b²c = 3bc²;

    30:6 = 5,   a³ : a³ = 1,   b² : b² = 1,   c² : c = c,

    30a³b²c² : 6a³b²c = 5c.

        В итоге: -12a⁴b³c + 18a³b³c³ - 30a³b²c² = - 6a³b²c·(2ab - 3bc² + 5c).

     А теперь сформулируем правило вынесения одночлена за скобки.

     Обратите внимание, что слагаемых в скобках после вынесения общего множителя должно быть столько, сколько в исходном многочлене.

И еще, старайтесь всегда после получения результата устно сделать проверку умножением, тогда вы никогда не допустите ошибку.

     И, в заключение, три интерактивных тренажера, чтобы отработать полученные знания на практике.

     Первый

      Второй тренажер немножко посложнее.

     Третий тренажер включает в себя теорию, практику и контрольное задание: