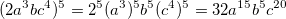Из всего многообразия треугольников, некоторые из них пользуются особым вниманием и любовью математиков. Это прямоугольные и равнобедренные треугольники. Чем же они отличаются от остальных и какими свойствами обладают?
Сначала поговорим о равнобедренном треугольнике. Дадим ему определение:


Как видите, у равнобедренного треугольника есть особые названия сторон: боковая - это одна из равных сторон, и основание - это третья сторона. Будьте внимательны при их определении, потому что треугольники могут быть расположены по разному:



Вершиной равнобедренного треугольника является та вершина, которая лежит напротив основания. В нашем случае - это точка В. Угол, лежащий напротив основания - угол при вершине равнобедренного треугольника.
Два другие угла — углы при основании равнобедренного треугольника. Углы при основании равнобедренного треугольника всегда острые
Чем же так хорош равнобедренный треугольник и что отличает его от остальных собратьев. Об этом нам говорят
Но теперь возникает другой вопрос: А как узнать, будет ли треугольник равнобедренным? Или, как говорят математики, каковы признаки равнобедренного треугольника? Вот они:
- Если два угла в треугольнике равны, то этот треугольник равнобедренный.
- Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, то он является равнобедренным.
Посмотреть доказательства приведенных теорем и порешать задачи можно на сайте "Школьный помощник" (помните, что для этого вы должны пройти регистрацию).